Orbital mechanics is a fun subject, as it involves a lot of seemingly empty space that’s nevertheless full of very real forces, all of which must be taken into account lest one’s spacecraft ends up performing a sudden lithobraking maneuver into a planet or other significant collection of matter in said mostly empty space. The primary concern here is that of gravitational pull, and the way it affects one’s trajectory and velocity. With a single planet providing said gravitational pull this is quite straightforward to determine, but add in another body (like the Moon) and things get trickier. Add another big planetary body (or a star like our Sun), and you suddenly got yourself the restricted three-body problem, which has vexed mathematicians and others for centuries.

The three-body problem concerns the initial positions and velocities of three point masses. As they orbit each other and one tries to calculate their trajectories using Newton’s laws of motion and law of universal gravitation (or their later equivalents), the finding is that of a chaotic system, without a closed-form solution. In the context of orbital mechanics involving the Earth, Moon and Sun this is rather annoying, but in 1772 Joseph-Louis Lagrange found a family of solutions in which the three masses form an equilateral triangle at each instant. Together with earlier work by Leonhard Euler led to the discovery of what today are known as Lagrangian (or Lagrange) points.

Having a few spots in an N-body configuration where you can be reasonably certain that your spacecraft won’t suddenly bugger off into weird directions that necessitate position corrections using wasteful thruster activations is definitely a plus. This is why especially space-based observatories such as the James Webb Space Telescope love to hang around in these spots.

Stable and Unstable Stable

Although the definition of Lagrange points often makes it sound like you can put a spacecraft in that location and it’ll remain there forever, it’s essential to remember that ‘stationary’ only makes sense in particular observer’s reference frame. The Moon orbits the Earth, which orbits the Sun, which ultimately orbits the center of the Milky Way, which moves relative to other galaxies. Or it’s just the expansion of space-time which make it appear that the Milky Way moves, but that gets one quickly into the fun corners of theoretical physics.

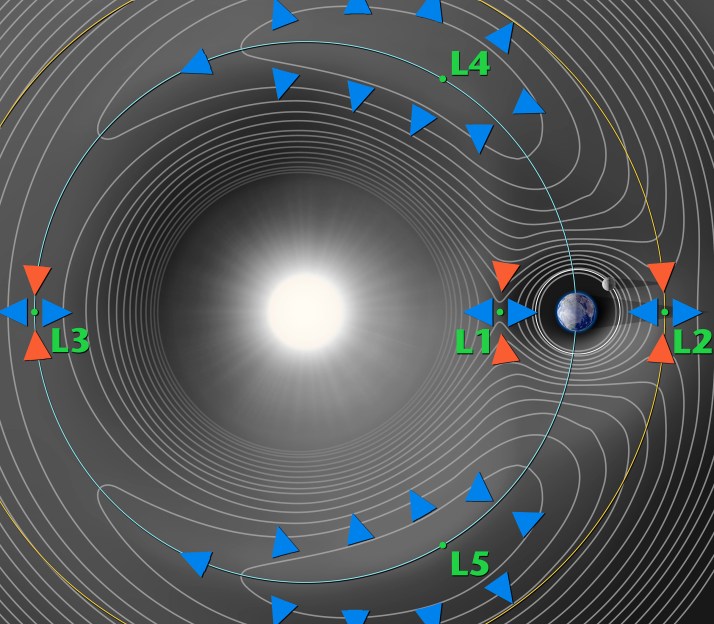
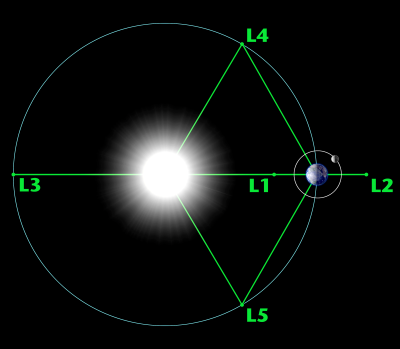
Within the Earth-Sun system, there are five Lagrange points (L1 – L5), of which L2 is currently the home of the James Webb Space Telescope (JWST) and was the home to previous observatories (like the NASA WMAP spacecraft) that benefit from always being in the shadow of the Earth. Similarly, L1 is ideal for any Sun observatory, as like L2 it is located within easy communication distance

Perhaps shockingly, the L3 point is not very useful to put any observatories or other spacecraft, as the Sun would always block communication with Earth. What L3 has in common with L1 and L2 is that all of these are unstable Lagrange points, requiring course and attitude adjustments approximately every 23 days. This contrasts with L4 and L5, which are the two ‘stable’ points. This can be observed in the above contour plot, where L4 and L5 are on top of ‘hills’ and L1 through L3 are on ‘saddles’ where the potential curves up in one direction and down another.

One way to look at it is that satellites placed in the unstable points have a tendency to ‘wander off’, as they don’t have such a wide region of relatively little variance (contour lines placed far from each other) as L4 and L5 do. While this makes these stable points look amazing, they are not as close to Earth as L1 and L2, and they have a minor complication in the fact that they are already occupied, much like the Earth-Moon L4 and L5 points.

Because of how stable the L4 and L5 points are, the Earth-Moon system ones have found themselves home to the Kordylewski clouds. These are effectively concentrations of dust which were first photographed by Polish astronomer Kazimierz Kordylewski in 1961 and confirmed multiple times since. Although a very faint phenomenon, there are numerous examples of objects caught at these points in e.g. the Sun-Neptune system (Neptune trojans) and the Sun-Mars system (Mars trojans). Even our Earth has picked up a couple over the years, many of them asteroids. Of note that is the Earth’s Moon is not in either of these Lagrange points, having become gravitationally bound as a satellite.

All of which is a long way to say that it’s okay to put spacecraft in L4 and L5 points as long as you don’t mind fragile technology sharing the same region of space as some very large rocks, with an occasional new rocky friend getting drawn into the Lagrange point.

Stuff in Lagrange Points

A quick look at the Wikipedia list of objects at Lagrange points provides a long list past and current natural and artificial objects at these locations, across a variety of system. Sticking to just the things that we humans have built and sent into the Final Frontier, we can see that only the Sun-Earth and Earth-Moon systems have so far seen their Lagrange points collect more than space rocks and dust.

Starting with Sun-Earth, the L1 point has:

• Solar and Heliospheric Observatory (SOHO, ESA)
• Advanced Composition Explorer (ACE, NASA)
• Global Geospace Science WIND (GGS, NASA)
• Deep Space Climate Observatory (DSCOVR, NOAA)
• Aditya-L1 (ISRO)

These will be joined  if things go well by IMAP in 2025 along with SWFO-L1, NEO Surveyor in 2027. These spacecraft mostly image the Sun, monitor solar wind, image the Earth and its weather patterns, for which this L1 point is rather excellent. Of note here is that strictly taken most of these do not simply linger at the L1 point, but rather follow a Lissajous orbit around said Lagrange point. This particular orbital trajectory was designed to compensate for the instability of the L1-3 points and minimize the need for course corrections.

Moving on, the Sun-Earth L2 point is also rather busy:

• Gaia space observatory (ESA)
• Spektr-RG astrophysics observatory (Russian-German)
• James Webb Space Telescope (JWST, NASA, ESA, CSA)
• Euclid space telescope (ESA)
• Chang’e 6 orbiter (CNSA)

Many of the planned spacecraft that should be joining the L2 point are also observatories for a wide range of missions, ranging from general observations in a wide range of spectra to exoplanet and comet hunting.

Despite the distance and hazards of the Sun-Earth L4 and L5 points, these host the Solar TErrestrial RElations Observatory (STEREO) A and B solar observation spacecraft. The OSIRIS-REx and Hayabusa 2 spacecraft have passed through or near one of these points during their missions. The only spacecraft planned to be positioned at one of these points is ESA’s Vigil, which is scheduled to launch by 2031 and will be at L5.

 

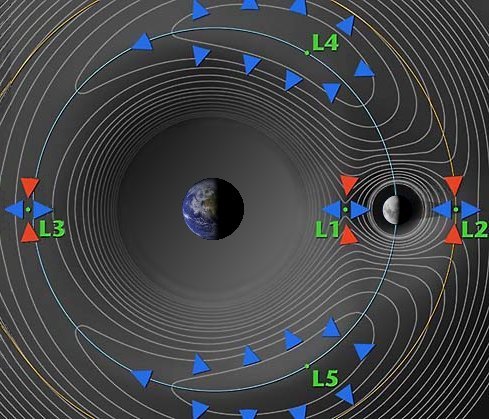
Only the Moon’s L2 point currently has a number of spacecraft crowding about, with NASA’s THEMIS satellites going through their extended mission observations, alongside the Chinese relay satellite Queqiao-2 which supported the Chang’e 6 sample retrieval mission.

In terms of upcoming spacecraft to join the sparse Moon Lagrange crowd, the Exploration Gateway Platform was a Boeing-proposed lunar space station, but it was discarded in favor of the Lunar Gateway which will be placed in a polar near-rectilinear halo orbit (NRHO) with an orbital period of about 7 days. This means that this space station will cover more of the Moon’s orbit rather than remain stationary. It is intended to be launched in 2027, as part of the NASA Artemis program.

Orbital Mechanics Fun

The best part of orbits is that you have so many to pick from, allowing you to not only pick the ideal spot to idle at if that’s the mission profile, but also to transition between them such as when traveling from the Earth to the Moon with e.g. a trans-lunar injection (TLI) maneuver. This involves a low Earth orbit (LEO) which transitions into a powered, high eccentric orbit which approaches the Moon’s gravitational sphere of influence.

Within this and low-energy transfer alternatives the restricted three-body problem continuously applies, meaning that the calculations for such a transfer have to account for as many variables as possible, while in the knowledge that there is no perfect solution. With our current knowledge level we can only bask in the predictable peace and quiet that are the Lagrange points, if moving away from all those nasty gravity wells like the Voyager spacecraft did is not an option.